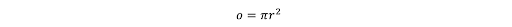Equation Poetry
By Radoslav Rochallyi
This article is about structural mathematical poetry, a particular kind of concrete poetry in which the typography and layout of the text emphasizes the overall effect. Although the theme of concrete poetry has been described a thousand times in countless places after the Guillaume Apollinaire era, there is still room for concrete poetry and the discovery of new forms. My goal is to introduce readers to a new type of concrete poetry called Equation Poetry. Equation Poetry uses mathematical language as an organizational principle and at the same time uses mathematical symbols to describe intonation notation (for example, nervous3) to define various types of specifications that are simpler or more efficient to express in non-text form, such as:
I do not consider mathematical poetry to be poetry about mathematics; the content of the poetry does not have mathematical meaning.
For me, mathematical poetry means poetry whose form is determined/defined by a mathematical rule, pattern, symbol, or structure—some kind of mathematical or geometric constraint. Poems with a mathematical structure do not necessarily have to be poems in the forms of a pyramid, a triangle, a square, or poems depicting real objects; they can also depict relations, as in equations.
A mathematical formula for the area of a circle:
Gives rise to this example of Equation Poetry:
The Taylor Series for ex:
Gives rise to this example of Equation Poetry:
If we take a closer look at poetry as such, we will find that every (or almost every) formal rule in poetry is a mathematical rule. This restriction defines the form of poetry. Hence, it can be said that (almost) no form of poetry can do without mathematics. Mathematics and poetry require great imagination. They both have symbolism, algorithmic basis, structures, formulas, and symmetry. Combining the two is completely natural, as is reading and studying their patterns.
Equation Poetry is characterized by a greater freedom of writing, or at least the possibility of choosing the equations used, which in itself defines the freedom of its creation. And it is clear that this is a freedom much greater than that provided by most of the strict structural forms.
I am convinced that the ambition of Equation Poetry should not be to preserve the meaning of the equation, but to preserve the form, formula and symmetry as accurately as possible. Preserving its full meaning would define the content of poetry and not just form. In such a case, we would not even be making poetry because the resulting poem would be a cluster of precisely positioned words, but without the general meaning. And we wouldn't be creating anything mathematical either; the resulting equation would simply not make sense.
Example of a Binomial Theorem Equation:
X= time
A= being
N= now
K= know
This is what strict Equation Poetry would look like. The reader will certainly acknowledge that this is not a poetic gem, and mathematically it has no meaning at all. However, it opens up new possibilities to express oneself, to discover, and to create.
Radoslav Rochallyi is a poet, essayist, and interdisciplinary artist living in Prague, Czech Republic. He is the author of eight books of poetry. His work has been featured in numerous publications.