How Will the New AI Impact Mathematics Research?

By Keith Devlin @KeithDevlin@fediscience.org, @profkeithdevlin.bsky.social

Will Large Language Models such as ChatGPT change how new mathematics is discovered? Yes. It’s happening already, just as occurred when earlier computing technologies came along: mechanical and then electronic calculators, general purpose digital computers, graphing calculators, etc. and more recently tools such as Mathematica, Maple, and (my favorite) Wolfram Alpha. (The latter three can lay claim to being a special kind of “artificial intelligence”, though as with chess-playing systems, the highly restricted nature of the domain means we don’t generally classify them as such.)

Are there problems in mathematics that humans can solve but AI can’t? I will argue that there are. Long standing open problems such as the Riemann Hypothesis may be examples of such. Proving this is, of course, not as straightforward, since it’s a universal negative. Indeed, you can’t prove such a claim. What we can do it reflect on the nature of mathematics and provide prima facie evidence that there are aspects to mathematical discovery that a LLM cannot achieve.

What is the case, however, is that use of LLMs might well (my guess is “will”, and soon) provide valuable assistance to human mathematicians in tackling major open problems (like the RH). The key to doing this is to identify what LLMs bring to mathematics that is new (and in some cases unique to them) and what parts of mathematical thinking they cannot do.

As always, since mathematical thinking is an extremal case of human thinking, this analysis will surely shine light on the kinds of changes to other aspects of our lives that may result from LLMs.

First, a bit of history. (It’s a personal-perspective history, but it serves to provide some of the background to my argument about LLMs.) The current frenzy for AI occasioned by the success of Large Language Models such as ChatGPT is at least the fourth “AI revolution” I’ve lived through. I say “at least” because the count depends on what you view as an “AI revolution”. Pretty well every generation of students who learn about mathematical logic (I’ll take that as a filter, since it applies even for approaches to AI that are not logic based) is seduced by the alure of “machines that think”. Even those of us who realize that machines (as we know and can build today) don’t actually think, can be intrigued by the possibility of creating machines that are capable of useful forms of “ersatz-thinking”.

Front cover (left) of the October 1950 issue of the academic journal MIND in which Alan Turing’s famous paper on “thinking machines” (first page shown right) was published.

I was born too late to be seduced by the first AI wave, started by mathematician and computer pioneer Alan Turing in his 1950 paper Computing Machinery and Intelligence, published in the academic philosophy journal MIND. Turing began his article with the sentence, I propose to consider the question, “Can machines think?”

From today’s perspective, the most salient feature of his essay is that he began by acknowledging the need for definitions of “machine” and “think”, and presented a proposal for a procedure to settle the question relative to those definitions (his famous “Turing Test”). No AI system has passed it, but they have gotten to perform much better. One factor at play is the human proclivity to ascribe intelligent agency to any system that exhibits a (remarkably) few features of human-like behavior; for example, see the 1996 book The Media Equation by my (more recent) Stanford colleagues Byron Reeves and the late Clifford Nass.

Shortly after Turing’s paper appeared, in 1956 John McCarthy organized a small scientific meeting at Dartmouth College, generally credited as marking the foundation of the academic (research and engineering) discipline of artificial intelligence (AI), in the process giving it that name.

(I knew McCarthy, and once entertained him in my home; the closest I got to Turing was a logician colleague who had been one of his students.)

That initial AI revolution, with a theoretical basis of formal logic, eventually became known as GOFAI, “good old-fashioned AI”. That was the first of many attempts to develop “thinking machines”, with each new approach being launched with the prediction that the goals would be met in about twenty-five years.

Failure to meet the lofty goals was, it must be said, balanced by each push leading to real advances in technologies that we now take for granted in many aspects of our lives. Pursuing big goals and failing to achieve them is always a good strategy for advancement.

In my case, after I graduated in mathematics from King’s College London in 1968 (during my time at which I had summer jobs at BP Chemicals programming mainframe computers in Algol-60 and assembly language), I went to the University of Bristol, intending to do a PhD in Computation Theory, a subject just beginning to emerge, of which AI was a part. I quickly switched tracks, when the primitive state of that research area was blindingly outshone by an explosion of activity in axiomatic set theory, started by Paul Cohen’s 1963 discovery of a method to prove (some kinds of) mathematical statements are undecidable.

(As a young mathematician just starting out, I was eager to work on “deep, hard problems”. I was too young to realize that mathematical “hardness” can come in different forms and proving theorems wasn’t the only major goal.) It would be almost twenty years before I returned to my original interest in what can be done with computers.

Part of my ongoing lack of excitement towards AI, in particular, came early on in my career, from reading Hubert Dreyfus’s book What Computers Can’t Do. Published in 1972, the year after I got my doctorate (in set theory) Dreyfus’s critique was dismissed by many at the time, but for me his points rang true, and still do.

With my interest in computers and AI rekindled by the release of the Apple Macintosh Computer in 1984 (I was an instant WIMP fan, and could see major uses in mathematics), I accepted an invitation to join a research team at the British technology company Logica working on a project funded by the Alvey Programme, a major UK initiative to develop (primarily) AI technologies (under a different name: Intelligent Knowledge-Based Systems, IKBS), in response to Japan’s “Fifth Generation Computer Programme”.

My participation did not last long. The Dreyfus critique seemed to me to be as pertinent as ever. But by then, I had experienced sufficient exposure to recent, exciting developments in natural language processing and the use of digital devices to mediate human interactions, to see those as promising domains where AI technologies might work. (For me, the key was using AI technologies to complement human intelligence, not replace it.) There was also the recent success of Parallel Distributed Processing, as described in the 1987 book with that title by David Rumelhart and Jay McClelland; that really excited me (because it was trying to model how the brain works).

My rekindled interest led to an invitation from Stanford to join a multi-disciplinary project doing exactly the kind of research I was trying to pursue. So, in the summer of 1987, my family and I packed our bags (two each) and flew to California (initially for a year). We never returned home. Much of my research career since then has involved trying to develop mathematical techniques (“mathematically-based” is a more accurate description) to handle aspects of reasoning and communication in a way that strives to respect the critiques levied by Dreyfus and a whole host of other scholars who followed him.

It was at Stanford that I met not only PDP’s Rumelhart (now deceased) and McClelland, but also Terry Winograd, a Stanford AI pioneer who had also crossed over to the “GOFAI-opposition”; a move that was surely not unconnected from his early-career AI focus of building physical robots, which meant his AI programs kept coming head-to-head with the unforgiving and not-to-be-misled real world. (See presently!)

I also got to know Stanford psychologist and psycholinguist Herb Clark, and then began a decade-long research collaboration with the UK-based sociolinguist and ethnographer Duska Rosenberg (who had gotten a second PhD in computer science — in part to be better-credentialed when she pushed back against critiques from her engineering colleagues at Brunel University in London, where she was at the time).

That collaboration with Rosenberg resulted in what I regard as my best mathematical work by far (the second decade of which was with other, US-based collaborators), though none of it was published in mathematics journals. (It’s mathematical, but not mathematics, as generally conceived. I kept my membership of the mainstream mathematics community alive by writing about the subject, through my involvement in mathematics education, and by an ongoing interest in mathematical cognition.)

The work I did after 1987, and especially those Stanford connections and my work with Rosenberg, immersed me in far too much evidence about people, language, and society to be seduced by the glitz of ChatGPT when it burst onto the scene a few months ago. And there is no doubt about it, the brightness of the glitz surprised everyone, even those who had built the system. (But it was just glitz. Take note of the computational linguist Emily Bender, who was a PhD student at Stanford, whose supervisor is a good friend of mine. Her writings about LLMs are spot on. Her description “stochastic parrot” to describe LLMs is both highly accurate and a wonderful meme to focus attention on the core of the “Can LLMs think?” issue.)

Which brings me to the role I see for LLMs in mathematical praxis and in mathematics research.

Why LLMs (and AI in general) will not replace human mathematicians

Figure 1. The landscape of mathematical activity. Mathematics advances by searching for patterns. Humans work with understanding across the entire space; LLMs work ***only*** in the top region (though they can examine a much bigger search space), but without understanding.

For all its abstraction, mathematics is firmly rooted in the physical and social world. Its fundamental concepts are not arbitrary inventions; they are, indeed, abstractions from the world.

That process of abstraction goes back to the very beginnings of mathematics, with the emergence of numbers around 10,000 years ago in Sumeria. I recounted that history in an online presentation for the New York based Museum of Mathematics on June 28 last year. You have to pay MoMath to view it (or the entire four-part series it was part of), but supporting the museum is a worthy cause!

In fact, numbers are arguably the most basic of mathematical abstractions. (Well, you could make a case for the notion of an abstract (sic) set being more basic, but historically numbers were abstracted millennia earlier. To be sure, today’s abstract numbers are defined and constructed from abstract sets, but the numbers we use today, including the counting numbers — often introduced to children as points on a number line — are a late 19th early 20th Century creation.

For most of history, counting numbers were multitude-species pairs having their origin in monetary systems (as with our “4 dollars and 90 cents” currency numbers). The transition from those early numbers into today’s pure abstractions began in the 17th Century with Descartes, Harriott, Newton and others and was completed only with the work of Peano and others in the late 19th Century and Frege, Russell, Hilbert, von Neumann and others in the early 20th Century. (Negative numbers were not accepted as bona fide mathematical objects until the 19th Century.)

The above paragraph a simplification of a long evolutionary process, but it serves to indicate the way we build abstractions on abstractions. The link between a mathematical abstraction to its origin in the world is usually a tower. (See Figure 1.)

The many abstract entities of modern mathematics, such as groups, rings, fields, Hilbert spaces, Banach spaces, and so on, are all connected to the real world by towers of abstractions. For all its seemingly esoteric nature, mathematics is firmly rooted in the real world. That’s why mathematical results can be applied to the real world; for example, theorems about geometric structures of dimension 4 and greater can be (and are) applied to solve real-world problems about communications networks, transportation networks, and efficient data storage.

Though we mathematicians are comfortable working within that world of abstractions, we achieve that comfort by first (as students) ascending the towers, which means the meanings we ascribe to the concepts are grounded in reality — even if we are not consciously aware of that grounding. (Mathematicians, perhaps more so than many other people, are very aware of how little we understand what is going on in our minds, even when deeply engaged in problem-solving thought. That recognition is forced on us every time we get a breakthrough idea “out of nowhere”!)

[Yes, last month’s post was planted to set the scene of this one, although what I say here is independent of the thesis advanced in that post.]

Mathematics is, then, a semantic enterprise engaged in by creatures/minds that are deeply and fundamentally connected to reality, and which have motivations, desires, curiosity, and a drive to understand both the world and one another. In terms of the figure, we operate in the entire space shown in that landscape. Mathematical knowledge results from activity we engage in as such creatures using the concepts and methods that we and our predecessors have abstracted from the world.

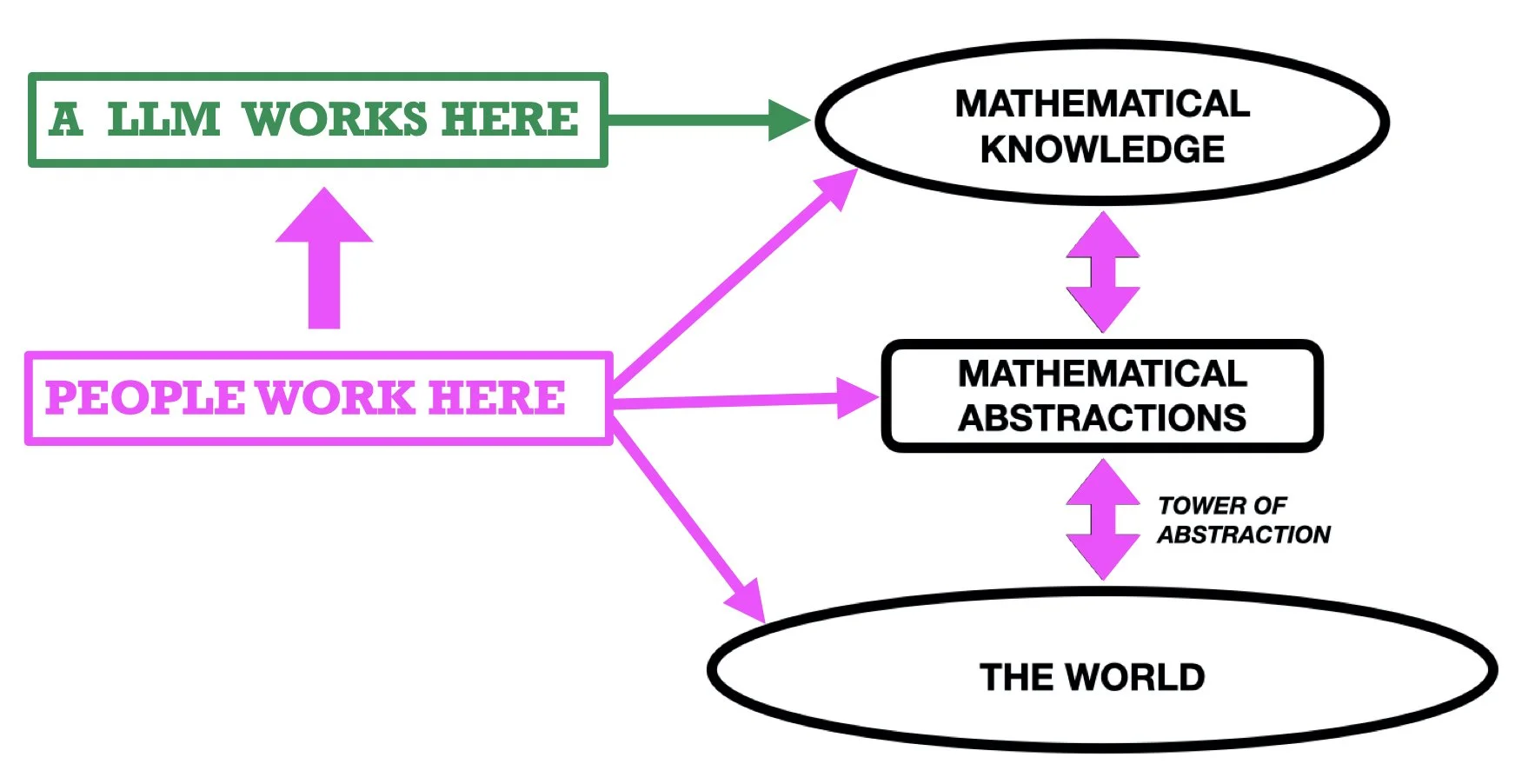
LLMs, in contrast, operate exclusively in the upper region, MATHEMATICAL KNOWLEDGE. They process text. Not meanings, text (i.e., strings of symbols). Whereas we humans can make advances by seeing patterns in the semantic entities we are studying, LLMs (implicitly) discern patterns in the symbols they process. Those patterns reflect the popularity of the symbols in a vast corpus of text produced by humans (and, increasingly, their own earlier productions and those of other LLMs, which may turn out to be a major problem for them and us). See Figure 2.

Figure 2. The magenta arrows indicate where people operate when doing mathematics. LLMs are restricted to operate (at the level of syntax) entirely on mathematical text. The vertical magenta arrow on the left indicates how we human mathematicians can put LLMs to work for us, if we so choose.

For the most part, their productions are correct because most of the texts they draw upon are correct – especially if the LLM is restricted to draw on sources that have passed through some form of review and editorial control. (Is this the case?) But as is already now well known, they can produce outputs that seem sensible but on examination are total nonsense. (For many applications, that’s a major negative, but for mathematics it is not a big problem. We are capable of detecting errors, and it’s usually pretty clear cut.)

This, I think, is a major weakness in LLMs as “thinking machines”. Even when our head is in the mathematical clouds, we humans have our feet firmly on the ground. (Metaphorically; many of us curl up on a comfy chair to ruminate.) We are living creatures of the world and we are an interactive part of the world, with brains that evolved to act in, react to, and think about the world. An LLM inputs and outputs strings of symbols. Period. Those are vastly different kinds of activity. [See the appendix for a summary of current work in cognitive science on how we think.]

Anyone who thinks this is not a huge distinction should spend some time in the library to immerse themselves in the vast literature stored under the sign “HUMANITIES”. (Also, see my aside above about Winograd and his early AI work on robotics.) The fact that we can give meaning to LLMs’ outputs reflects our cognitive abilities, not theirs; they are just doing what we built them to do. (Much like the clocks we build; a clock does not have a concept of time; we construct clocks so that we can interpret their state as the time.) Using words like “intelligence” or “thinking” for AI systems is a category error. LLMs do something different from us. (Think of them as a very fancy analogue of a clock, designed to report on the current state of the human knowledge stored on the Internet.) We should view them as such.

What I find particularly intriguing is the possibility that a LLM will detect a pattern in the current corpus of mathematical knowledge that we humans are unlikely to discern — except perhaps by the kind of one-off chance encounter of two (or more) researchers who discover each knows something of relevance to the other. (The mathematical folklore is full of such instances that have led to major advances. Here’s one example of a cross-disciplinary encounter.) This, to my mind, is one way LLMs can benefit mathematical research. Indeed, it’s not impossible (though perhaps highly unlikely) that an LLM could produce an original result this way, perhaps giving the world “ChatGPT-7’s Theorem”.

More likely, it seems to me, is LLMs making mathematicians aware of (human or written) sources they did not know about. (LLMs as “dating apps for mathematicians trying to prove theorems” anyone?) We can of course do that already using a search engine; indeed, many of us use Google as a first port-of-call when starting on a new problem, as I’ve noted before in this venue. But the LLM brings something new: the capacity to discern syntactic (i.e., symbolic) patterns in the vast corpus of written mathematics that humans are (for reasons of scale, if nothing else) not capable of discerning. Many of those patterns may turn out to have no mathematical import. But some may. That’s something we have never had before.

NOTE: In my May, June, and July posts last year, I discussed the already-established power of LLMs as a front-end for mathematical systems such as Wolfram Alpha.

APPENDIX: How we think

[A more accurate heading would be “How we think we think”.]

Though we have been surprised at the performance of the more recent LLMs, we designed them and we know how they work, down to the fine detail. In contrast, we have no real knowledge of how our minds work. We did not design them. It’s by no means certain our current state of scientific knowledge is capable of (ever) describing, let alone explaining, how our minds work. In fact, there is a strong, natural selection argument to be made that we will never have conscious access to the “inner workings” of our mind. (See the Devlin’s Angle essays for January and February 2023.)

The best we can do is list some features of how we think.* Insofar as mathematical thought is just a highly restricted form of human thought (as language and music are restricted forms of human communication), these considerations will provide a starting point for speculating how we do mathematics.

Humans possess perception and action systems that intervene on the external world and generate new information about it.
Those action systems utilize causal representations that are embodied in theories (scientific or intuitive) and are also the result of truth-seeking epistemic processes.
Those theories are evaluated with respect to an external world and make predictions about and shape actions in that world; new evidence from that world can radically revise them.
Causal representations, such as perceptual representations, are designed to solve “the inverse problem”: reconstructing the structure of a novel, changing, external world from the data that we receive from that world.
Although such representations may be very abstract, as in scientific theories, they ultimately depend on perception and action—on being able to perceive the world and act on it in new ways.
Cultural evolution depends on the balance between two different kinds of cognitive mechanisms. Imitation allows the transmission of knowledge or skill from one person to another. Innovation produces novel knowledge or skill through contact with a changing world.
Imitation means that each individual agent does not have to innovate—they can take advantage of the cognitive discoveries of others. But imitation by itself would be useless if some agents did not also have the capacity to innovate. It is the combination of the two that allows cultural and technological progress.

Contrast the above considerations with a LLM, which aggregates large amounts of information that have been generated by people and uses relatively simple statistical inference to extract patterns from that information.

The design of an LLM allows for the production of information we were not previously aware of, and we may sometimes be surprised by the results we get. Nevertheless (in contrast to the human mind) we understand the mechanism of production, down to the fine detail.

Nothing in the training or objective functions of a LLM is designed to fulfill the epistemic functions of truth-seeking systems such as perception, causal inference, or theory formation.

That leaves them with the role of (potentially-) useful tools for our individual and societal use. That may turn out to be progress. This new tool may change the way we live and work; if so, then likely in ways that will surprise us (maybe even horrify us, at least initially).

As with any tool that has “hidden parts”, however, it is critical that anyone who uses it understands how it works, what its limitations are, and what dangers those limitations can lead to. Bender’s wonderful term “stochastic parrots” first appeared in a 2021 research paper titled On the Dangers of Stochastic Parrots: Can Language Models Be Too Big? Note that word “dangers”. (The paper appeared before ChatGPT burst onto the scene.)

In that paper the authors laid out a number of real dangers to society that LLMs present. As those dangers manifest (it has already started), society may seek to impose strict controls. It could be that one of the few real benefits of this new AI is to mathematical, scientific, and engineering knowledge, where truth and the real world are unshakable metrics. (The issue of effects on the communities of mathematicians, scientists, and engineers is altogether different; there the dangers pointed out by Bender et al are particularly acute.)

Our species’ history is full of such developments, and when one occurs there is no going back. This may be an Oppenheimer moment.

* Reference: There’s a mass of literature on the issue described above. I’ll cite one recent paper that provides an initial gateway to that literature. I used it as a reference source for my outline (especially the bulleted list):

Eunice Yiu , Eliza Kosoy, and Alison Gopnik, Transmission Versus Truth, Imitation Versus Innovation: What Children Can Do That Large Language and Language-and-Vision Models Cannot (Yet), Association for Psychological Science: Perspectives on Psychological Science , 2023, pp.1–10, National Institutes of Health, DOI 10.1177/17456916231201401.